Una titulación ácido-base es una técnica de cuantificación de la materia, la cual permite conocer la concentración de un ácido o una base en disolución, a partir de su equilibrio de neutralización, en donde el analito (muestra problema en disolución con concentración desconocida) reacciona con una cantidad equivalente de titulante (disolución de ácido o base de concentración conocida con un alto índice de certidumbre). La evaluación de la reacción de neutralización entre un ácido y una base puede inspeccionarse mediante la construcción de una curva de titulación, con la cual se visualiza la variación de pH antes, durante y después de la neutralización. Una curva de titulación ácido base es una gráfica donde se muestra el valor del pH de la solución en función del volumen de titulante agregado. El titulante siempre debe ser un ácido fuerte o una base fuerte. El analito puede ser ya sea una base o ácido fuerte o una base o ácido débil. En el caso de un ácido fuerte contra una base fuerte, tanto el titulante como el analito están por completo ionizados. Un ejemplo es la titulación de ácido clorhídrico con hidróxido de sodio:
$$HCl + NaOH \rightleftarrows H_2O + NaCl$$
$$H^+ + Cl^- + Na^+ + OH^- \rightleftarrows H_2O + Na^+ + Cl^-$$
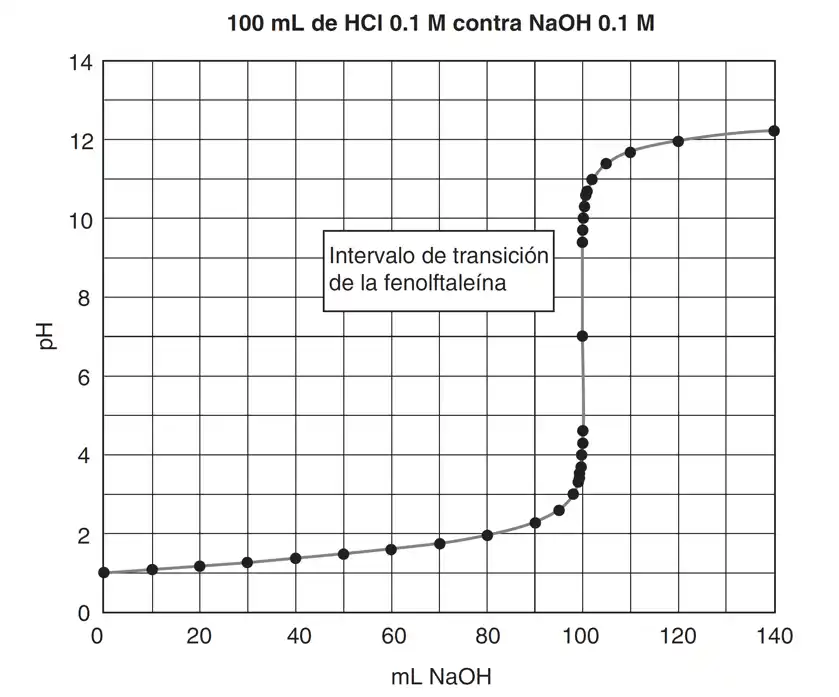
Los iones $H^+$ y el $OH^-$ se combinan para formar $H_2O$ y los iones $Na^+$ y $Cl^-$ permanecen intactos, de manera que el resultado total de la neutralización es la conversión del $HCl$ en una solución neutra de $NaCl$. En la Figura 1 se muestra la curva de titulación para 100 ml de una solución 0.1 M de $HCl$ titulada con una solución 0.1 M de $NaOH$.
Los cálculos de las curvas de titulación consisten en el cálculo del pH a partir de la concentración de las especies particulares presentes en las diversas etapas de la titulación. Se deben emplear cambios de volumen durante la titulación para determinar la concentración de las especies.
Una curva de titulación ácido base es una gráfica donde se muestra el valor del pH de la solución en función del volumen de titulante agregado.
A continuación se explican las diferentes etapas de una curva de titulación en las regiones más importantes para el caso anterior.
1. Al principio de la titulación, se tiene HCl 0.1 M, de modo que el pH inicial es 1.
2. Al avanzar la titulación, parte del $H^+$ reacciona para encontrarse como $H_2O$, de modo que la concentración de $H^+$ disminuye gradualmente.
3. Al 90% de la neutralización (90 mL de $NaOH$), sólo queda el 10% del $H^+$ . Ignorando el cambio de volumen, la concentración de $H^+$ en este punto sería $10^{-2}$ M y el pH habría aumentado en sólo una unidad de pH (si se corrige por cambio de volumen, será ligeramente mayor). Sin embargo, al acercarse al punto de equivalencia (el punto en el que se agrega una cantidad estequiométrica de la base), la concentración de $H^+$ se reduce rápidamente hasta que, en el punto de equivalencia, cuando la neutralización es completa, queda una solución neutra de $NaCl$ y el pH es 7.0.
4. Al continuar agregando $NaOH$, la concentración de $OH^-$ aumenta rápidamente desde $10^{-7}$ M en el punto de equivalencia y se nivela entre $10^{-2}$ y $10^{-1}$ M, entonces se tiene una solución de $NaOH$ más $NaCl$. Así, el pH permanece apreciablemente constante a un lado y otro del punto de equivalencia, pero cambia en forma notable muy cerca del punto de equivalencia. Este gran cambio permite definir la terminación de la reacción midiendo ya sea el pH o alguna propiedad que cambie con el pH.
Ejemplo:
Calcular el pH a 0, 10, 90, 100 y 110% de la titulación de 50.0 mL de $HCl$ 0.100 M con $NaOH$ 0.100 M.
Solución:
Al 0%:
$$pH = -log(0.100) = 1.00$$
Al 10%:
Se han agregado 5.0 mL de $NaOH$. Se comienza con 0.100 M X 50.0 mL = 5.00 mmol de $H^+$.
Calcular la concentración de $H^+$ después de agregar el $NaOH$:
$$\text{mmol } H^+ \text{ al inicio} = 5.00 \text{ mmol } H^+$$
$$\text{mmol } OH^- \text{ agregados} = 0.100 M \times 5.0 \text{ mL} = 0.500 \text{ mmol } OH^-$$
$$\text{mmol } H^+ \text{ remanentes} = 4.50 \text{ mmol } H^+ \text{en } 55.0 \text{ mL}$$
$$[H^+] = \frac{4.50 \text{ mmol }}{55.0 \text{ mL}} = 0.0818 M$$
$$pH = -log(0.0818) = 1.09$$
Al 90%:
$$\text{mmol } H^+ \text{ al inicio} = 5.00 \text{ mmol } H^+$$
$$\text{mmol } OH^- \text{ agregados} = 0.100 M \times 45.0 \text{ mL} = 4.500 \text{ mmol } OH^-$$
$$\text{mmol } H^+ \text{ remanentes} = 0.50 \text{ mmol } H^+ \text{ en } 95.0 \text{ mL}$$
$$[H^+] = 0.00526 M$$
$$pH = -log(0.00526) = 2.28$$
Al 100%:
Todo el $H^+$ ha reaccionado con $OH^-$ y se tiene una solución 0.0500 M de $NaCl$.
Por tanto, el pH es 7.00.
Al 110%:
Ahora se tiene una solución que consiste en NaCl y el exceso de NaOH agregado.
$$\text{mmol } OH^- = 0.100 M \times 5.0 \text{ mL} = 0.500 \text{ mmol } OH^- \text{ en } 105 \text{ mL}$$
$$[OH^-] = 0.00476 M$$
$$pOH = -log(0.00476) = 2.32$$
$$pH = 14 - pOH = 11.68$$
Obsérvese que antes del punto de equivalencia, cuando hay ácido en exceso, la relación es:
$$[H^+] = \frac{ M_{\acute{a}cido} \times V_{\acute{a}cido} \times M_{base} \times V_{base} }{ V_{total} }$$
Donde $V$ es el volumen. Esto se puede aplicar simplemente para calcular $[H^+]$ una vez que se haya entendido la resolución de este ejemplo.
De igual manera, más allá del punto de equivalencia, cuando hay exceso de base la relación es:
$$[OH^-] = \frac{M_{base} \times V_{base} \times M_{\acute{a}cido} \times V_{\acute{a}cido} }{ V_{total} }$$
Referencias:
1. Skoog D. A., West D. M., Holler F. J., Crouch S. R.; (2014) Fundamentals of Analytical Chemistry; Ninth Edition; United States; CENGAGE Learning;.
2. Skoog D. A., Holler F. J., Crouch S. R.; (2007) Principles of Instrumental Analysis; Sixth Edition; United States; CENGAGE Learning;.
3. Christian G. D.; (2009) Analytical Chemistry; Sixth Edition; Washington, USA; McGraw Hill;.
4. Harris D. C.; (2016) Quantitative Chemical Analysis; Sixth Edition; California, USA; Reverté Editorial.

